Researchers have developed a new computer system that will allow computers to complete complex tasks quicker than they currently do.
A new computer system aims to solve some of the computing world’s hardest challenges in record time.
Researchers from the Georgia Institute of Technology and the University of Notre Dame have taken cues from the human brain in creating a new system that employs a network of electronic oscillators to solve graph coloring tasks in a fraction of the time.
“We wanted to find a way to solve a problem without using the normal binary representations that have been the backbone of computing for decades,” Arijit Raychowdhury, an associate professor in Georgia Tech’s School of Electrical and Computer Engineering, said in a statement. “Applications today are demanding faster and faster computers to help solve challenges like resource allocation, machine learning and protein structure analysis—problems which at their core are closely related to graph coloring.
“But for the most part, we’ve reached the limitations of modern digital computer processors,” he added. “Some of these problems are so computationally difficult to perform, it could take a computer several weeks to solve.”
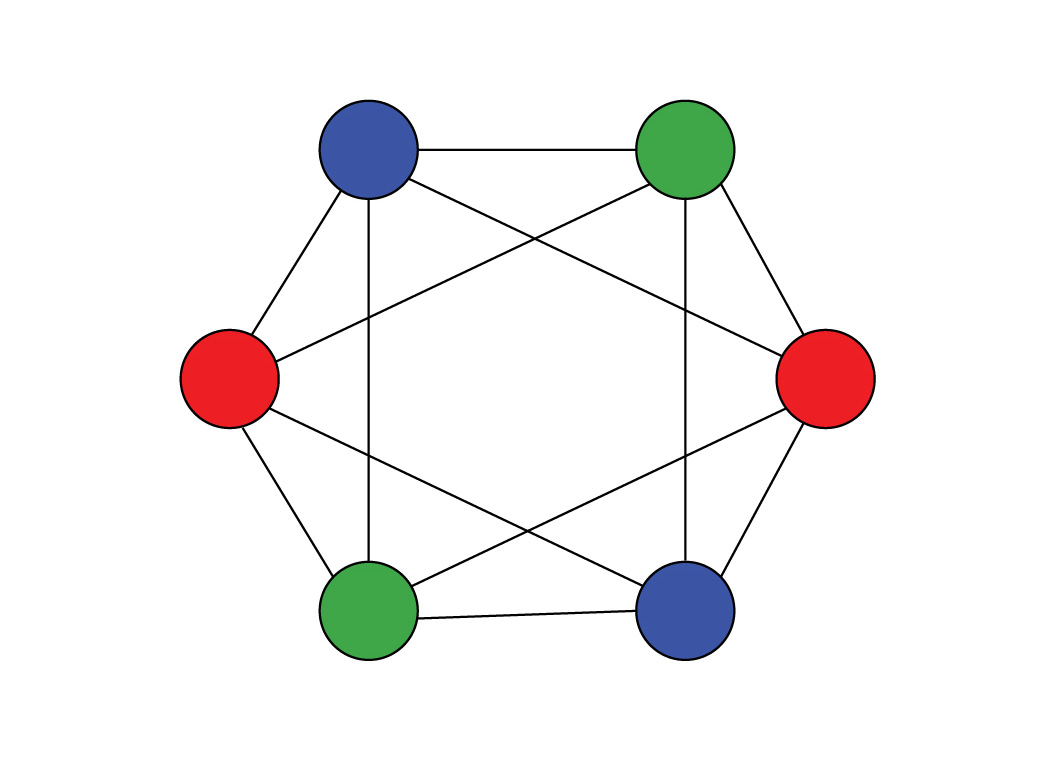
A graph coloring system begins with a graph—a visual representation of a set of objects connected in some way and the computer solves the problem by assigning each object a color. However, two objects directly connected cannot share the same color, the aim being to color all objects in the graph using the smallest number of different colors.
The researchers created a system similar to the human brain, where processing is handled collectively, such as a neural oscillatory network, rather than with a central processor.
“It’s the notion that there is tremendous power in collective computing,” Suman Datta, Chang Family professor in Notre Dame’s College of Engineering and one of the study’s co-authors, said in a statement. “In natural forms of computing, dynamical systems with complex interdependencies evolve rapidly and solve complex sets of equations in a massively parallel fashion.”
The electronic oscillators are fabricated from vanadium dioxide and were found to have a natural ability that could be used for graph coloring problems. A group of oscillators automatically synchronized to the same frequency when they were electrically connected through capacitive links.
At the same time the oscillators directly connected to one another operate at different phases within the same frequency and oscillators in the same group that are not directly connected would sync in both frequency and phase.
“If you suppose that each phase represents a different color, this system was essentially mimicking naturally the solution to a graph coloring problem,” Raychowdhury said.
The researchers created a small network of oscillators with the same number objects that theoretically proved that a connection existed between graph coloring and the natural dynamics of coupled oscillatory systems.
“This is a critical step because we can prove why this is happening and that it covers all possible instances of graphs,” Raychowdhury said. “This opens up a new way of performative computation and constructing novel computational models.
“This is novel in that it’s a physics-based computing approach, but it also presents tantalizing opportunities for building other customized analog systems for solving hard problems efficiently.”
The researchers now plan on building a larger network of oscillators that could handle graph coloring problems with more objects at play.
“Our goal is to reach a system with hundreds of oscillators, which would put us in striking distance of developing a computing substrate that could solve graph coloring problems whose optimal solutions are not yet known to mankind,” Datta said.
The study was published in Scientific Reports.